- Obtener vínculo
- X
- Correo electrónico
- Otras apps
- Obtener vínculo
- X
- Correo electrónico
- Otras apps
Ejercicios resueltos de sistemas de ecuaciones lineales con dos incognitas Aquí

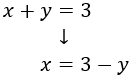 Y la sustituimos en la segunda:
Y la sustituimos en la segunda:
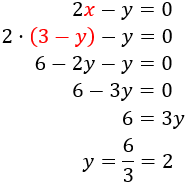 Calculamos x sabiendo y:
Calculamos x sabiendo y:
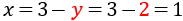 Por tanto, la solución del sistema es
Por tanto, la solución del sistema es
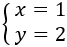
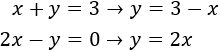 Como y = y, igualamos las expresiones y resolvemos la ecuación:
Como y = y, igualamos las expresiones y resolvemos la ecuación:
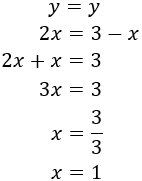 Ahora, sustituimos el valor de la incógnita x = 1 en la primera de las ecuaciones anteriores para obtener y:
Ahora, sustituimos el valor de la incógnita x = 1 en la primera de las ecuaciones anteriores para obtener y:
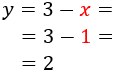 Por tanto, la solución del sistema es
Por tanto, la solución del sistema es
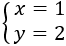
Después, sumamos las ecuaciones y resolvemos la ecuación obtenida:
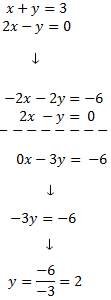 Finalmente, sustituimos el valor de y = 2 en la primera ecuación y la resolvemos:
Finalmente, sustituimos el valor de y = 2 en la primera ecuación y la resolvemos:
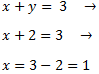 Por tanto, la solución del sistema de ecuaciones es
Por tanto, la solución del sistema de ecuaciones es
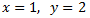
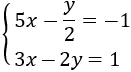
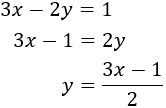 Sustituimos la expresión obtenida en la primera ecuación y la resolvemos:
Sustituimos la expresión obtenida en la primera ecuación y la resolvemos:
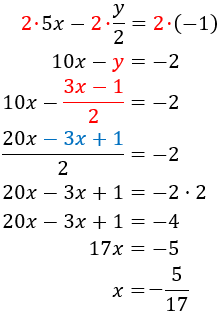 Como ya conocemos x, calulamos y sustituyendo en alguna de las ecuaciones anteriores:
Como ya conocemos x, calulamos y sustituyendo en alguna de las ecuaciones anteriores:
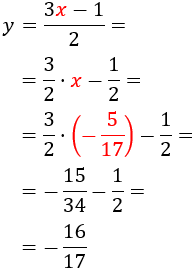 Por tanto, la solución del sistema es
Por tanto, la solución del sistema es
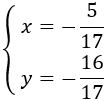
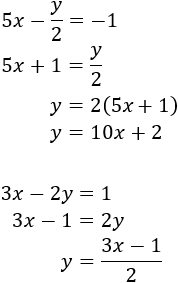 Igualamos las expresiones y resolvemos la ecuación:
Igualamos las expresiones y resolvemos la ecuación:
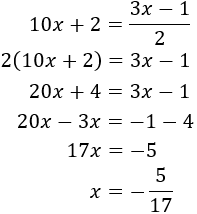 Sustituyendo x en la primera de las ecuaciones anteriores obtenemos y:
Sustituyendo x en la primera de las ecuaciones anteriores obtenemos y:
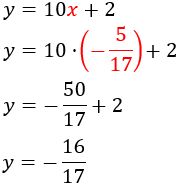 Por tanto, la solución del sistema es
Por tanto, la solución del sistema es
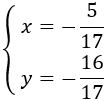
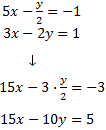 Cambiamos el signo a la segunda ecuación (la multiplicamos por -1) y sumamos las ecuaciones:
Cambiamos el signo a la segunda ecuación (la multiplicamos por -1) y sumamos las ecuaciones:
 Sustituimos el valor de y en la primera ecuación y la resolvemos:
Sustituimos el valor de y en la primera ecuación y la resolvemos:
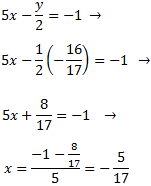 Por tanto, la solución del sistema es
Por tanto, la solución del sistema es
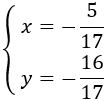
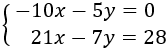
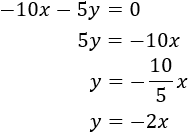 Sustituimos su expresión en la segunda ecuación y la resolvemos:
Sustituimos su expresión en la segunda ecuación y la resolvemos:
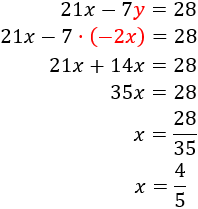 Calculamos y sabiendo x:
Calculamos y sabiendo x:
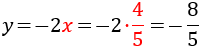 Por tanto, la solución del sistema es
Por tanto, la solución del sistema es
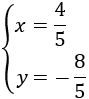
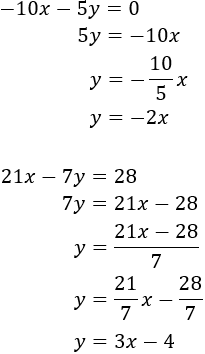 Igualamos las expresiones obtenidas y resolvemos la ecuación:
Igualamos las expresiones obtenidas y resolvemos la ecuación:
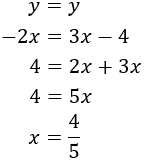 Sustituyendo en la primera de las ecuaciones anteriores obtenemos:
Sustituyendo en la primera de las ecuaciones anteriores obtenemos:
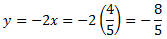 Por tanto, la solución del sistema es
Por tanto, la solución del sistema es
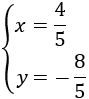
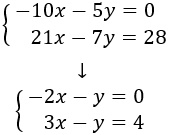 De este modo evitamos coeficientes altos que complican las operaciones. Ahora multiplicamos la primera ecuación por 3, la segunda por 2 y las sumamos:
De este modo evitamos coeficientes altos que complican las operaciones. Ahora multiplicamos la primera ecuación por 3, la segunda por 2 y las sumamos:
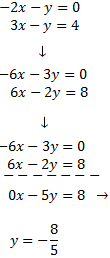 Sustituimos el valor de y en la primera ecuación y la resolvemos:
Sustituimos el valor de y en la primera ecuación y la resolvemos:
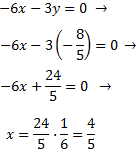 Por tanto, la solución del sistema es
Por tanto, la solución del sistema es
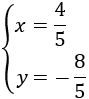
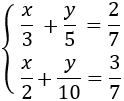
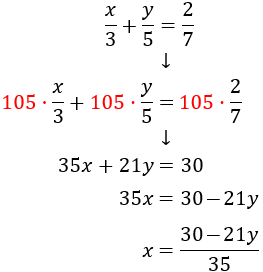 Sustituimos en la segunda ecuación la x y la resolvemos. Primero multiplicamos por el mínimo común múltiplo de los denominadores:
Sustituimos en la segunda ecuación la x y la resolvemos. Primero multiplicamos por el mínimo común múltiplo de los denominadores:
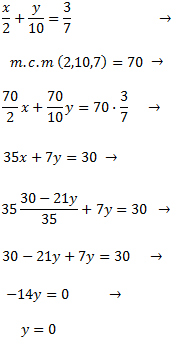 Calculamos y sabiendo x:
Calculamos y sabiendo x:
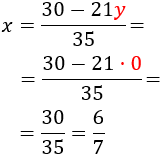 Por tanto, la solución del sistema es
Por tanto, la solución del sistema es
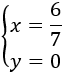
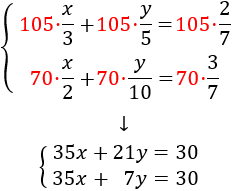 Despejamos en las dos ecuaciones la x:
Despejamos en las dos ecuaciones la x:
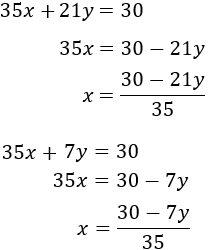 Igualamos ambas expresiones y resolvemos la ecuación:
Igualamos ambas expresiones y resolvemos la ecuación:
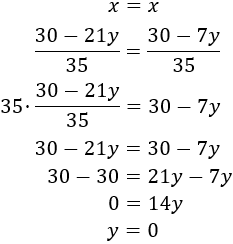 Sustituyendo en la primera de las ecuaciones anteriores:
Sustituyendo en la primera de las ecuaciones anteriores:
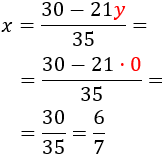 Por tanto, la solución del sistema es
Por tanto, la solución del sistema es
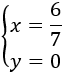
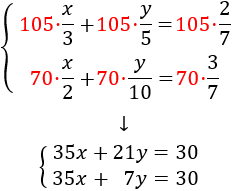 Multiplicamos la segunda por -1 y sumamos las ecuaciones:
Multiplicamos la segunda por -1 y sumamos las ecuaciones:
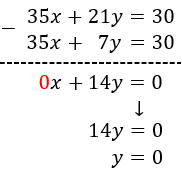 Sustituimos el valor de y en la primera ecuación y la resolvemos:
Sustituimos el valor de y en la primera ecuación y la resolvemos:
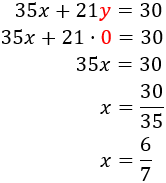 Por tanto, la solución del sistema es
Por tanto, la solución del sistema es
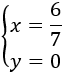
Un sistema de ecuaciones lineales es un conjunto de ecuaciones (lineales) que tienen más de una incógnita. Las incógnitas aparecen en varias de las ecuaciones, pero no necesariamente en todas. Lo que hacen estas ecuaciones es relacionar las incógnitas entre sí.
Por ejemplo:
{3x+2y=1x−5y=6
Se trata de un sistema de dos ecuaciones con dos incógnitas (x e y).
Resolver un sistema de ecuacionesconsiste en encontrar el valor de cada incógnita para que se cumplan todas las ecuaciones del sistema.
La solución al sistema del ejemplo es
x=1y=−1
Pero no siempre existe solución, o bien, pueden existir infinitas soluciones. Si hay una única solución (un valor para cada incógnita, como en el ejemplo anterior) se dice que el sistema es compatible determinado. No hablaremos de los otros tipos ya que en esta sección sólo se estudian los sistemas determinados.
Para resolver un sistema (compatible determinado) necesitamos tener al menos tantas ecuaciones como incógnitas.
En esta sección resolvemos sistemas (lineales) de dos ecuaciones con dos incógnitas mediante los métodos que describimos a continuación, que se basan en la obtención de una ecuación de primer grado.
- sustitución: consiste en despejar o aislar una de las incógnitas (por ejemplo, x) y sustituir su expresión en la otra ecuación. De este modo, obtendremos una ecuación de primer grado con la otra incógnita, y. Una vez resuelta, obtenemos el valor de xsustituyendo el valor de y que ya conocemos.
- reducción: consiste en operar con las ecuaciones como, por ejemplo, sumar o restar ambas ecuaciones, de modo que una de las incógnitas desaparezca. Así obtenemos una ecuación con una sola incógnita.
- igualación: consiste en aislar en ambas ecuaciones la misma incógnita para poder igualar las expresiones, obteniendo así una sola ecuación con una incógnita.
No olvidemos que si multiplicamos una ecuación por un número distinto de 0, la ecuación inicial y la obtenida son equivalentes. Esto quiere decir que ambas ecuaciones tienen las mismas soluciones y, por tanto, podemos trabajar con una u otra. Usaremos esta propiedad con frecuencia en el método de reducción.
4 Sistemas de Ecuaciones resueltos
Por sustitución, igualación y reducción.
Sistema 1

Ver Solución
SOLUCIÓN POR SUSTITUCIÓN
Despejamos en la primera ecuación la x: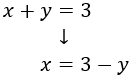
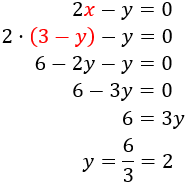
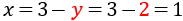
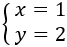
SOLUCIÓN POR IGUALACIÓN
Despejamos en ambas ecuaciones la y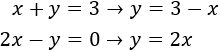
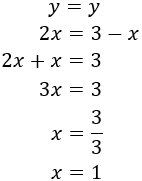
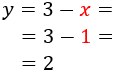
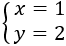
SOLUCIÓN POR REDUCCIÓN
Para sumar las ecuaciones y que desaparezca una de las dos incógnitas, los coeficientes de dicha incógnita deben ser iguales pero de signo distinto. Para ello, multiplicamos por -2 la primera ecuación.Después, sumamos las ecuaciones y resolvemos la ecuación obtenida:
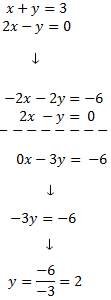
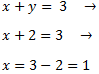
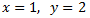
Sistema 2
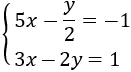
Ver Solución
SOLUCIÓN POR SUSTITUCIÓN
Despejamos en la segunda ecuación la y: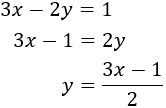
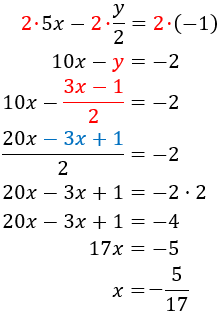
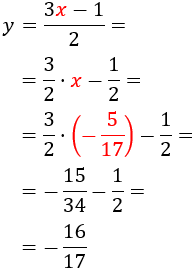
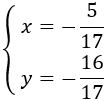
SOLUCIÓN POR IGUALACIÓN
Despejamos en ambas ecuaciones la y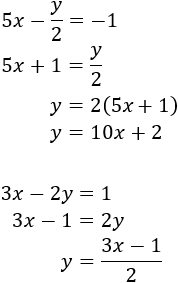
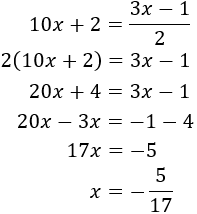
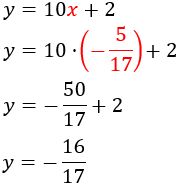
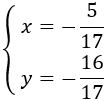
SOLUCIÓN POR REDUCCIÓN
Multiplicamos la primera ecuación por 3 y la segunda por 5 para conseguir que el coeficiente de la incógnita x tenga el mismo coeficiente en ambas ecuaciones: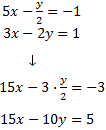

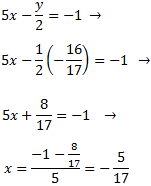
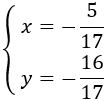
Sistema 3
Ver Solución
SOLUCIÓN POR SUSTITUCIÓN
Despejamos en la primera ecuación la y: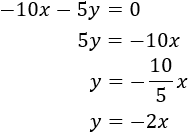
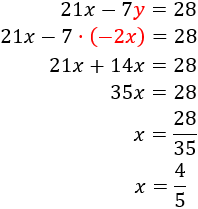
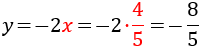
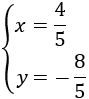
SOLUCIÓN POR IGUALACIÓN
Despejamos en ambas ecuaciones la y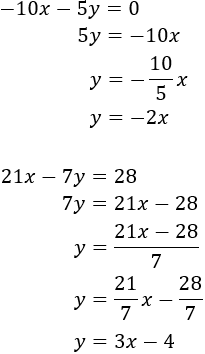
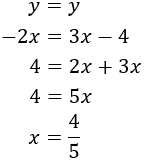
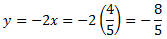
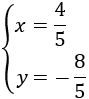
SOLUCIÓN POR REDUCCIÓN
Multiplicamos la primera ecuación por 1/5 y la segunda por 1/7: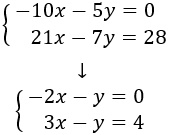
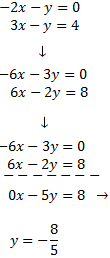
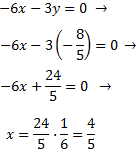
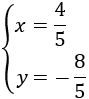
Sistema 4
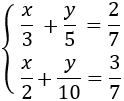
Ver Solució
SOLUCIÓN POR SUSTITUCIÓN
Despejamos de la primera ecuación la x. Pero, primero, multiplicamos la ecuación por el mínimo común múltiplo de los denominadores y, de este modo, evitamos las fracciones.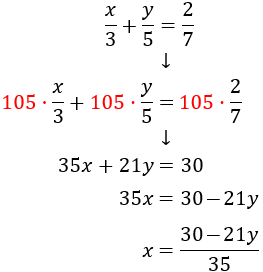
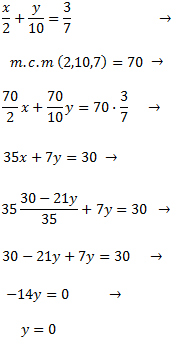
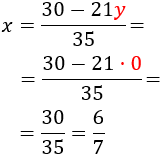
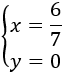
SOLUCIÓN POR IGUALACIÓN
Multiplicamos cada ecuación por el mínimo común múltiplo de sus denominadores obteniendo las ecuaciones: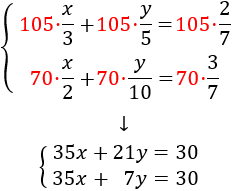
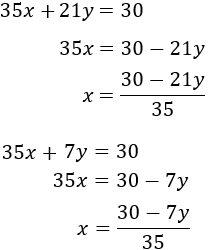
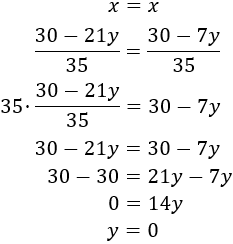
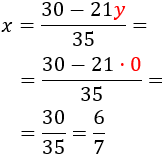
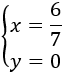
SOLUCIÓN POR REDUCCIÓN
Multiplicamos cada ecuación por el mínimo común múltiplo de sus denominadores obteniendo las ecuaciones: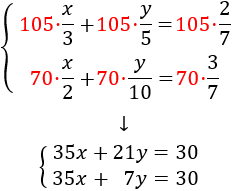
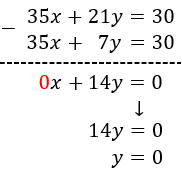
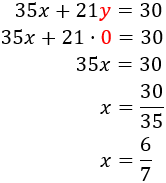
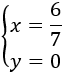

Comentarios
Publicar un comentario