- Obtener vínculo
- X
- Correo electrónico
- Otras apps
- Obtener vínculo
- X
- Correo electrónico
- Otras apps
Mediante
una balanza de torsión, Coulomb encontró que la fuerza de atracción o repulsión
entre dos cargas puntuales (cuerpos cargados cuyas dimensiones son
despreciables comparadas con la distancia r que las separa) es
inversamente proporcional al cuadrado de la distancia que las separa.
El valor
de la constante de proporcionalidad depende de las unidades en las que se
exprese F, q, q’ y r. En
el Sistema Internacional de Unidades de Medida vale 9·109 Nm2/C2.
Obsérvese
que la ley de Coulomb tiene la misma forma funcional que la ley
de la Gravitación Universal
El
electroscopio consta de dos láminas delgadas de oro o aluminio A que están
fijas en el extremo de una varilla metálica B que pasa a través de un soporte
C de ebonita, ámbar o azufre. Cuando se toca la bola del electroscopio con un
cuerpo cargado, las hojas adquieren carga del mismo signo y se repelen siendo
su divergencia una medida de la cantidad de carga que ha recibido. La fuerza
de repulsión electrostática se equilibra con el peso de las hojas.
|
Si se
aplica una diferencia de potencial entre la bola C y la caja del mismo, las
hojas también se separan. Se puede calibrar el electroscopio trazando la curva
que nos da la diferencia de potencial en función del ángulo de divergencia.
Un modelo
simplificado de electroscopio consiste en dos pequeñas esferas de masa m cargadas
con cargas iguales q y del mismo signo que cuelgan de dos
hilos de longitud d, tal como se indica la figura. A partir de la
medida del ángulo q que forma una bolita con la vertical, se
calcula su carga q.
|
|
Sobre
una bolita actúan tres fuerzas
|
En el
equilibrio
Tsenq =F
Tcosq =mg
Tcosq =mg
- Conocido el ángulo θ determinar
la carga q
Dividiendo
la primera ecuación entre la segunda, eliminamos la tensión T y
obtenemos
F=mg·tanθ
Midiendo
el ángulo θ obtenemos la fuerza de repulsión F entre
las dos esferas cargadas
De acuerdo
con la ley de Coulomb
Calculamos
el valor de la carga q, si se conoce la longitud d del
hilo que sostiene las esferas cargadas.
- Conocida la carga q determinar
el ángulo θ
Eliminado T en
las ecuaciones de equilibrio, obtenemos la ecuación
La
carga q está en mC y la masa m de
la bolita en g.
Expresando
el coseno en función del seno, llegamos a la siguiente ecuación cúbica
El
programa interactivo, calcula las raíces de la ecuación
cúbica
En la
figura, se muestra el comportamiento de un electroscopio, para cada carga q en μC ten
En
términos matemáticos, esta ley se refiere a la magnitud F de la fuerza que cada
una de las dos cargas puntuales q 1 y q 2 ejerce
sobre la otra separadas por una distancia r y se expresa
en forma de ecuación como:
k es una constante conocida
como constante Coulomb y las barras denotan valor
absoluto .
F es el vector Fuerza que sufren las
cargas eléctricas. Puede ser de atracción o de repulsión, dependiendo del signo
que aparezca (en función de que las cargas sean positivas o negativas).
- Si las
cargas son de signo opuesto (+ y –), la fuerza "F"
será negativa, lo que indica atracción
- Si las
cargas son del mismo signo (– y – ó + y +), la fuerza "F"
será positiva, lo que indica repulsión .
En el gráfico vemos que, independiente del signo que ellas posean, las fuerzas se ejercen siempre en la misma dirección (paralela a la línea que representa r), tienen siempre igual módulo o valor (q 1 x q 2 = q 2 x q 1 ) y siempre se ejercen en sentido contrario entre ellas.
Ejemplo:
.- Una
carga de 3×10^-6 C se encuentra 2 m de una carga de -8×10^-6 C, ¿Cuál es la
magnitud de la fuerza de atracción entre las cargas?
Solución:
Para darle solución al ejercicio, debemos de obtener los datos para poder
resolverlo de manera directa, puesto que tenemos todo lo que necesitamos.
$\displaystyle
{{q}_{1}}=3x{{10}^{-6}}$C
$\displaystyle
{{q}_{2}}=-8x{{10}^{-6}}$C
$\displaystyle
d=2m$
$\displaystyle
K=9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}}$
Aplicando
la fórmula de la ley de coulomb
$\displaystyle
F=K\frac{{{q}_{1}}\cdot {{q}_{2}}}{{{d}^{2}}}$
Sustituimos
$\displaystyle
F=\left[ 9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}}$ $\right]\frac{(3x{{10}^{-6}}C)\cdot
(-8x{{10}^{-6}}C)}{{{(2m)}^{2}}}$
$\displaystyle
F=\left[ 9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}}
\right]\frac{-24x{{10}^{-12}}{{C}^{2}}}{4{{m}^{2}}}$
Hemos
multiplicado las cargas eléctricas, recordar que los exponentes se suman. y hemos
elevado al cuadrado la distancia que los separa, ahora seguimos con las
operaciones.
$\displaystyle
F=\left[ 9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}}$ $\right]-6x{{10}^{-12}}\frac{{{C}^{2}}}{{{m}^{2}}}$
Multiplicamos
y obtenemos:
$\displaystyle
F=-54x{{10}^{-3}}N=-0.054N$
Vemos que
hay un signo negativo, por ahora no nos sirve interpretar el signo, puesto que
el problema nos pide la magnitud de la fuerza, esto quiere decir que tomaremos
la fuerza como un valor absoluto, que vendría a ser nuestro resultado.
$\displaystyle
F=0.054N$
Ejemplo 2:
La
magnitud de la fuerza de atracción o repulsión que experimentan dos cargas
eléctricas, es directamente proporcional al producto de las cargas e
inversamente proporcional al cuadrado de la distancia que los separa.
Suena algo
confuso ¿cierto?, la cuestión es entenderlo, por ahora no te preocupes sino
entendiste lo del enunciado, esto en términos matemáticos se expresa de la
siguiente manera:
$\displaystyle
F=K\frac{{{q}_{1}}\cdot {{q}_{2}}}{{{d}^{2}}}$
dónde:
$\displaystyle
{{q}_{1}},{{q}_{2}} = Cargas eléctricas [Coulomb]$
$\displaystyle
F = Fuerza [Newton]$
$\displaystyle
d = Distancia [Metros]$
$\displaystyle
K=9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}} = Constante de Coulomb$
Gráficamente
lo podemos ver de la siguiente forma:
Esto
quiere decir, que podemos saber la fuerza de atracción o repulsión de las
cargas eléctricas, respecto a la distancia a la que estén separadas, o
alejadas. Esto es fácil de entender, y si te has dado cuenta, es similar a ley
de la gravitación universal. Por lo que
podemos deducir que:





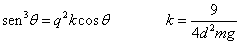




Comentarios
Publicar un comentario